［文字サイズの変更］▼▲
 
数学クラブ
三平方の定理
定期試験対策テスト    時間 50分        1/11 ページ
点
1
次の問に答えなさい．
1
2点×4
(1) xの値を求めなさい．   [381-00]
 1
 
35
 
 
 x
 
(2) xの値を求めなさい．   [381-00]
 3
 
3
 3
 
 x
 
(3) xの値を求めなさい．   [381-00]
 2
 
 5
 
 x
 
(4) 次の長さを３辺とする三角形のうち，直角三角形はどれですか．   [382-00]
    (ア)  
 3，2，5
 
    (イ)  
10
 1，3，
 
    (ウ)  
 2，3，4
 
    (エ)  
3
6
 1，，
 

(1)
(2)
(3)
(4)
@2025    http://sugaku.club/
 
 
数学クラブ
三平方の定理
定期試験対策テスト        2/11 ページ
2
次の問に答えなさい．   [380-00]
2
11点 部分点可
∠C＝90°の直角三角形ABCと合同な三角形を，次の図のように並べます．四角形ABHGと四角形CDEFが正方形であることから，a2＋b2＝c2となることを証明しなさい．
A
B
C
D
E
F
G
H
a
b
c
空欄に記入
@2025    http://sugaku.club/
 
 
数学クラブ
三平方の定理
定期試験対策テスト        3/11 ページ
3
次の問に答えなさい．
3
2点×4
(1) 次の長方形の対角線の長さを求めなさい．    [383-00]
 2
 
2
 4
 
(2) ２辺の長さがの三角形があります．
 2cm，4cm
 
この三角形が直角三角形であるためには，残りの１辺の長さは，何cmであればよいですか．   [384-00]
(3) １辺の長さが
7
の
 
 
正三角形ABCの高さを求めなさい．   [390-00]
B
A
C
 h
 
7
 
 
(4) xの値を求めなさい．   [392-00]
 1
 
 x
 
30°
(1)
(2)
(3)
(4)
@2025    http://sugaku.club/
 
 
数学クラブ
三平方の定理
定期試験対策テスト        4/11 ページ
4
次の問に答えなさい．
4
3点×3
(1) 半径3cmの円があります．円Oの弦ABの長さが，4cmのとき，中心Oから弦ABまでの距離を求めなさい．   [393-00]
O
A
B
H
cm
 4
 
(2) １辺の長さがの
 1
 
正三角形ABCの面積を求めなさい．   [391-00]
B
A
C
 1
 
(3) 次の座標を持つ２点の間の距離を求めなさい．   [394-01]
 A(−8，−4)，B(−9，−2)
 
(1)
(2)
(3)
@2025    http://sugaku.club/
 
 
数学クラブ
三平方の定理
定期試験対策テスト        5/11 ページ
5
次の問に答えなさい．
5
4点×2
(1) 次の図で，APは，Pを接点とする円Oの接線です．xの値を求めなさい．   [395-00]
A
P
O
 2
 
 x
 
 6
 
(2) xの値を求めなさい．   [396-00]
C
45°
A
2
 
 
x
B
105°
(1)
(2)
@2025    http://sugaku.club/
 
 
数学クラブ
三平方の定理
定期試験対策テスト        6/11 ページ
6
次の問に答えなさい．
6
4点×2
(1) xの値を求めなさい．   [397-00]
A
B
C
H
 5
 
x
 4
 
 5
 

(2) xの値を求めなさい．   [397-10]
A
B
C
H
x
5
 3
 
 3
 
 3
 

(1)
(2)
@2025    http://sugaku.club/
 
 
数学クラブ
三平方の定理
定期試験対策テスト        7/11 ページ
7
次の問に答えなさい．
7
3点×3
次の図は直方体です．次の問に答えなさい．   [3A0-00]
A
B
C
D
E
F
G
H


１．ACの長さを AB，BCを使って求めなさい．




２．AGの長さを AB，BC，CGを使って求めなさい．









３．AB＝3cm ，BC＝5cm ，CG＝5cm のとき，AGの長さを求めなさい．
1
2
3
@2025    http://sugaku.club/
 
 
数学クラブ
三平方の定理
定期試験対策テスト        8/11 ページ
8
次の問に答えなさい．
8
3点×3
正四角錐OABCDがあります．底面ABCDは，１辺が5cm の正方形で，他の辺の長さは，すべて6cm です．次の問に答えなさい．   [3A2-00]
A
B
C
D
O
H
6cm
5cm


１．AHの長さを求めなさい．




２．OHの長さを求めなさい．










３．OABCDの体積を求めなさい．
1
2
3
@2025    http://sugaku.club/
 
 
数学クラブ
三平方の定理
定期試験対策テスト        9/11 ページ
9
次の問に答えなさい．   [3A3-20]
9
9点 部分点可
底面が半径 2cm の円形で，母線の長さが，4cm である円錐の体積を求めなさい．
A
O
H
4cm
2cm
@2025    http://sugaku.club/
 
 
数学クラブ
三平方の定理
定期試験対策テスト        10/11 ページ
10
次の問に答えなさい．   [3A4-20]
10
9点 部分点可
半径7cmの球Oを，中心Oから，6cmの距離にある平面で切った時，切り口の図形は円になります．この円の円周の長さを求めなさい．
O
A
H
cm
 6
 
@2025    http://sugaku.club/
 
 
数学クラブ
三平方の定理
定期試験対策テスト        11/11 ページ
11
次の問に答えなさい．   [3A4-30]
11
4点×3
１辺の長さが，6cm の立方体があります．３点 B，E，Gを通る平面でこの立方体を切るとき，次の問に答えなさい．
A
B
C
D
E
F
G
H

１．三角錐FBEGの体積を求めなさい．
２．△BEGの面積を求めなさい．








３．角錐FBEGの底面を△BEGと考えるとき，高さを求めなさい．
1
2
3
@2025    http://sugaku.club/
 
 
数学クラブ
【解答例】
定期試験対策テスト    時間 50分        1/11 ページ
1
次の問に答えなさい．
1
2点×4
(1) xの値を求めなさい．   [381-00]
 1
 
35
 
 
 x
 
    
2
2
35
2
 x=1＋=36
 
x＞0 だから
    
 x=6
 
(2) xの値を求めなさい．   [381-00]
 3
 
3
 3
 
 x
 
    
2
2
3
2
 x=3＋(3)=36
 
x＞0 だから
    
 x=6
 
(3) xの値を求めなさい．   [381-00]
 2
 
 5
 
 x
 
    
2
2
2
 x=2＋5=29
 
x＞0 だから
    
29
 x=
 
(4) 次の長さを３辺とする三角形のうち，直角三角形はどれですか．   [382-00]
    (ア)  
 3，2，5
 
    (イ)  
10
 1，3，
 
    (ウ)  
 2，3，4
 
    (エ)  
3
6
 1，，
 

(ア)
2
2
2
 3＋2=13≠5
 
(イ)
2
2
10
2
    ◯
 1＋3=10=
 
(ウ)
2
2
2
 2＋3=13≠4
 
(エ)
2
3
2
2
6
2
 1＋=2≠
 
(1)
 6
 
(2)
 6
 
(3)
29
 
 
(4) イ
@2025    http://sugaku.club/
 
 
数学クラブ
【解答例】
定期試験対策テスト        2/11 ページ
2
次の問に答えなさい．   [380-00]
2
11点 部分点可
∠C＝90°の直角三角形ABCと合同な三角形を，次の図のように並べます．四角形ABHGと四角形CDEFが正方形であることから，a2＋b2＝c2となることを証明しなさい．
A
B
C
D
E
F
G
H
a
b
c
四角形CDEFの面積を S とする．
四角形CDEFは正方形だから，
    S＝(a＋b)2    ---①

また，四角形CDEFの面積は，４つの直角三角形と正方形ABHGに分けることができるから，
     1 
2
    ---②
 S=4×ab＋c
  2 

① ② から，
    
2
 (a＋b)
 
 1 
2
 =4×ab＋c
  2 
2
2
 a＋2ab＋b
 
2
 =2ab＋c
 
2
2
 a＋b
 
2
 =c
 
空欄に記入
@2025    http://sugaku.club/
 
 
数学クラブ
【解答例】
定期試験対策テスト        3/11 ページ
3
次の問に答えなさい．
3
2点×4
(1) 次の長方形の対角線の長さを求めなさい．    [383-00]
 2
 
2
 4
 
対角線の長さをx とする．
    
2
2
2
2
 x=2＋(4)=36
 
x＞0 だから
    
 x=6
 
(2) ２辺の長さがの三角形があります．
 2cm，4cm
 
この三角形が直角三角形であるためには，残りの１辺の長さは，何cmであればよいですか．   [384-00]
残りの１辺の長さをx cm とする．
直角をはさむ２辺の長さがのとき
 2cm，4cm
 
    
2
2
2
 x=2＋4=20
 
x＞0 だから
    
5
 x=2
 
   
斜辺の長さがのとき
 4cm
 
    
2
2
2
 x=4−2=12
 
x＞0 だから
    
3
 x=2
 
(3) １辺の長さが
7
の
 
 
正三角形ABCの高さを求めなさい．   [390-00]
B
A
C
 h
 
7
 
 
 1 
7
 
  2 
    
2
7
2
 1 
7
2
 21 
 h=−()=
  2  4 
x＞0 だから
     1 
21
 h=
  2 
(4) xの値を求めなさい．   [392-00]
 1
 
 x
 
30°
    
 1：x
 
3
 =1：
 
 x
 
3
 =
 
(1)
 6
 
(2)
5
3
 2cm，2cm
 
(3)
 1 
21
 
  2 
(4)
3
 
 
@2025    http://sugaku.club/
 
 
数学クラブ
【解答例】
定期試験対策テスト        4/11 ページ
4
次の問に答えなさい．
4
3点×3
(1) 半径3cmの円があります．円Oの弦ABの長さが，4cmのとき，中心Oから弦ABまでの距離を求めなさい．   [393-00]
O
A
B
H
cm
 4
 
cm
 3
 
x
    
2
2
2
 AO=OH＋AH
 
OHを x とすると．
    
2
2
2
 x=3−2=5
 
x＞0 だから
    
5
 x=
 
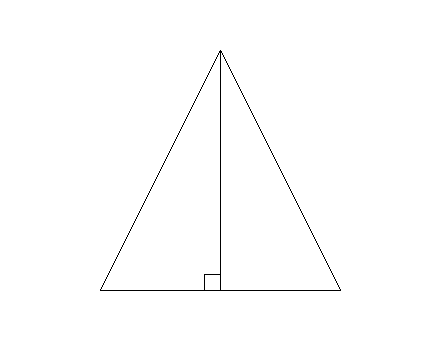
(2) １辺の長さがの
 1
 
正三角形ABCの面積を求めなさい．   [391-00]
B
A
C
 1
 
 h
 
 1 
 
  2 
    
2
2
 1 
2
 3 
 h=1−()=
  2  4 
h＞0 だから  1 
3
 h=
  2 
面積
 S
 
 1  1 
3
 =×1×
  2  2 
 S
 
 1 
3
 =
  4 
(3) 次の座標を持つ２点の間の距離を求めなさい．   [394-01]
 A(−8，−4)，B(−9，−2)
 
    
2
 AB
 
2
2
 ={−9−(−8)}＋{−2−(−4)}
 
 
 
2
2
 =(−1)＋2
 
2
 AB
 
 =5
 
AB＞0 だから
    
5
 AB=
 
(1)
5
cm
 
 
(2)
 1 
3
 
  4 
(3)
5
 
 
@2025    http://sugaku.club/
 
 
数学クラブ
【解答例】
定期試験対策テスト        5/11 ページ
5
次の問に答えなさい．
5
4点×2
(1) 次の図で，APは，Pを接点とする円Oの接線です．xの値を求めなさい．   [395-00]
A
P
O
 2
 
 x
 
 6
 
    
2
2
2
 x=6−2=32
 
x＞0 だから
    
2
 x=4
 
(2) xの値を求めなさい．   [396-00]
C
45°
A
2
 
 
x
B
H
30°
45°
60°
頂点BからCAに垂線を引き，その交点をHとする．
△BCHは，45°,45°,90°の直角二等辺三角形だから，
 BH=1
 
△BAHは，30°,60°,90°の直角三角形だから，
 x=2
 

(1)
2
 4
 
(2)
 2
 
@2025    http://sugaku.club/
 
 
数学クラブ
【解答例】
定期試験対策テスト        6/11 ページ
6
次の問に答えなさい．
6
4点×2
(1) xの値を求めなさい．   [397-00]
A
B
C
H
 5
 
x
 4
 
 5
 
直角三角形ABHについて，
    
2
 AH
 
2
2
 =5−4
 
2
 AH
 
 =9
 
直角三角形ACHについて，
    
2
 x
 
2
2
 =5＋AH
 
2
 x
 
 =34
 
x＞0 だから
    
34
 x=
 

(2) xの値を求めなさい．   [397-10]
A
B
C
H
x
5
 3
 
 3
 
 3
 
直角三角形ABHについて，
    
2
 AH
 
5
2
2
 =(3)−(3＋3)
 
2
 AH
 
 =9
 
直角三角形ACHについて，
    
2
 x
 
2
2
 =3＋AH
 
2
 x
 
 =18
 
x＞0 だから
    
2
 x=3
 

(1)
34
 
 
(2)
2
 3
 
@2025    http://sugaku.club/
 
 
数学クラブ
【解答例】
定期試験対策テスト        7/11 ページ
7
次の問に答えなさい．
7
3点×3
次の図は直方体です．次の問に答えなさい．   [3A0-00]
A
B
C
D
E
F
G
H


１．ACの長さを AB，BCを使って求めなさい．

△ABCの直角三角形から
    
2
2
2
        ---①
 AC=AB＋BC
 
AC＞0 だから
    
2
2
AB＋BC
 AC=
 



２．AGの長さを AB，BC，CGを使って求めなさい．

△ACGに着目すると，∠ACG＝90°だから
    
2
2
2
 AG=AC＋CG
 
①より
    
2
2
2
2
 AG=AB＋BC＋CG
 
AG＞0 だから
    
2
2
2
AB＋BC＋CG
 AG=
 


３．AB＝3cm ，BC＝5cm ，CG＝5cm のとき，AGの長さを求めなさい．
    
 AG
 
2
2
2
AB＋BC＋CG
 =
 
 AG
 
2
2
2
3＋5＋5
 =
 
 AG
 
59
 =
 
1
2
2
AB＋BC
 AC=
 
2
2
2
2
AB＋BC＋CG
 AG=
 
3
59
cm
 
 
@2025    http://sugaku.club/
 
 
数学クラブ
【解答例】
定期試験対策テスト        8/11 ページ
8
次の問に答えなさい．
8
3点×3
正四角錐OABCDがあります．底面ABCDは，１辺が5cm の正方形で，他の辺の長さは，すべて6cm です．次の問に答えなさい．   [3A2-00]
A
B
C
D
O
H
6cm
5cm


１．AHの長さを求めなさい．
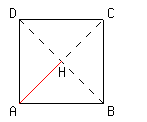正方形ABCDの対角線ACの長さは，
    
2
 AC=AB
 
正方形ABCDの対角線は，中点で交わるから，AHの長さは
    
 AH
 
 1 
 =AC
  2 
 
 
 1 
2
 =AB
  2 
 
 
 1 
2
 =×5
  2 
 AH
 
 5 
2
 =
  2 

２．OHの長さを求めなさい．
△OAHに着目すると，∠AHO＝90°だから
    
2
 OH
 
2
2
 =OA−AH
 
 
 
2
 5 
2
2
 =6−()
  2 
 
 
 47 
 =
  2 
OH＞0 だから
    
 OH
 
 47 
 2 
 =
 
 
 
 1 
94
 =
  2 

３．OABCDの体積を求めなさい．
正四角錐OABCDの体積をVとすると，
    
 V
 
 1 
2
 =ABOH
  3 
 
 
 1 
2
 1 
94
 =×5×
  3  2 
 
 
 25 
94
 =
  6 
1
  5 
2
cm
 
  2 
2
  1 
94
cm
 
  2 
3
  25 
94
cm3
 
  6 
@2025    http://sugaku.club/
 
 
数学クラブ
【解答例】
定期試験対策テスト        9/11 ページ
9
次の問に答えなさい．   [3A3-20]
9
9点 部分点可
底面が半径 2cm の円形で，母線の長さが，4cm である円錐の体積を求めなさい．
A
O
H
4cm
2cm

［OHの長さ(円錐の高さ)を求める］
    
2
 OH
 
2
2
 =OA−AH
 
 
 
2
2
 =4−2
 
 
 
 =16−4
 
 
 
 =12
 
OH＞0 だから
    
3
 OH=2
 


［円錐の体積を求める］
円錐の体積をVとすると，
 1     だから
 V=×底面積×高さ
  3 
    
 V
 
 1 
2
3
 =×π×2×2
  3 
 V
 
 8 
3
 =π
  3 

 8 
3
cm3
 π
  3 
@2025    http://sugaku.club/
 
 
数学クラブ
【解答例】
定期試験対策テスト        10/11 ページ
10
次の問に答えなさい．   [3A4-20]
10
9点 部分点可
半径7cmの球Oを，中心Oから，6cmの距離にある平面で切った時，切り口の図形は円になります．この円の円周の長さを求めなさい．
O
A
H
cm
 6
 
cm
 7
 


［切り口の円の半径を求める］
    
2
2
2
 AO=OH＋AH
 
AHを r とすると．
    
2
2
2
 r=7−6=13
 

r＞0 だから
    
13
 r=
 


［切り口の円周の長さ l を求める］
    
 l
 
 =2πr
 
 
 
13
 =2π×
 
 
 
13
 =2π
 
13
cm
 2π
 
@2025    http://sugaku.club/
 
 
数学クラブ
【解答例】
定期試験対策テスト        11/11 ページ
11
次の問に答えなさい．   [3A4-30]
11
4点×3
１辺の長さが，6cm の立方体があります．３点 B，E，Gを通る平面でこの立方体を切るとき，次の問に答えなさい．
A
B
C
D
E
F
G
H

１．三角錐FBEGの体積を求めなさい．
三角錐FBEGの底面を△BEFと考えると，高さはFGとなるから，三角錐FBEGの体積Vは．
 1 
 V=△BEF×FG
  3 
        
 △BEF
 
 1  1 
2
 =ABAE=×6=18
  2  2 
 V
 
 1 
 =△BEF×FG
  3 
 
 
 1 
 =×18×6=36
  3 
２．△BEGの面積を求めなさい．
E
G
B
x
2
 6
 
2
 3
 
△BEGは正三角形．一辺の長さは，正方形ABFEの対角線の長さだから，
    
2
 BE
 
2
2
 =AB＋AE
 
 BE
 
2
 =6
 
正三角形BEGの高さ x は，30°,60°,90°の直角三角形の辺の比から
    
 x
 
2
3
6
 =3×=3
 
△BEGの面積は，
    
 △BEG
 
 1 
 =BEx
  2 
 
 
 1 
2
6
3
 =×6×3=18
  2 
３．角錐FBEGの底面を△BEGと考えるとき，高さを求めなさい．
角錐FBEGの体積 V を，底面△BEGの面積と高さ h からもとめる．
    
 V
 
 1 
 =△BEGh
  3 
 h
 
3V
3
1
3
 ==3×36÷(18)=6=2
 
△BEG
3
1
 cm3
 36
 
2
 
3
cm2
 18
 
3
 
3
cm
 2
 
@2025    http://sugaku.club/