図形の性質と証明
定期試験対策テスト 時間 60分 1/14 ページ
点
1
次の空欄に適する語を書きなさい.
1
1点×6
| 空欄に記入 |
2
下図の三角形の中から合同な三角形の組を選び,記号≡を使って表しなさい.また,合同条件を書きなさい. [2L5-00]
2
順不同 完答 2点×3
8cm A B 14cm C | 4cm 35° D E F | 7cm 60° G H I |
4cm 35° J K L | 7cm 60° M N O | 8cm P Q 14cm R |
| (1) | |
| (2) | |
| (3) |
@2025 http://sugaku.club/
図形の性質と証明
定期試験対策テスト 2/14 ページ
3
次のことがらについて,逆を答えなさい.また,それが正しい場合には○,間違っている場合には×を( )に書きなさい.逆が間違っている場合に反例を書きなさい. [2J0-z3]
3
完答 1点×3
(1) 関数 y=3x−1 において x=1 ならば y=2 である.
(2) △ABCと△DEFについて AB=DE,BC=EF,AC=DF ならば △ABC≡△DEF である.
(3) △ABC≡△DEF ならば AB=DE である.
| (1) | 逆: ( ) 反例: |
| (2) | 逆: ( ) 反例: |
| (3) | 逆: ( ) 反例: |
4
次の空欄に適する語を書きなさい.
4
1点×4
| 空欄に記入 |
@2025 http://sugaku.club/
図形の性質と証明
定期試験対策テスト 3/14 ページ
5
次の問に答えなさい. [2i0-z0]
5
7点 部分点可
次の図で,AB=CBならば,∠A=∠Cであることを証明しなさい.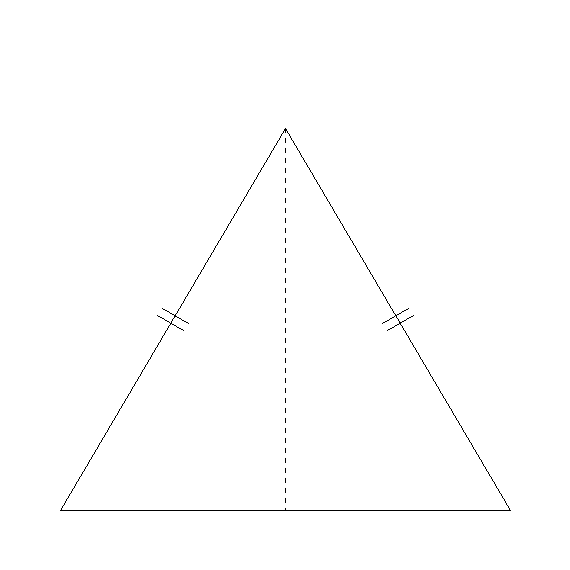

A
B
C
D
| 空欄に記入 |
@2025 http://sugaku.club/
図形の性質と証明
定期試験対策テスト 4/14 ページ
6
次の問に答えなさい. [2i2-z0]
6
7点 部分点可
△ABCの辺AB,AC上にそれぞれ点D,Eがあり,BD=CEとする.このとき,DC=EBならば,△ABCは二等辺三角形になることを証明しなさい.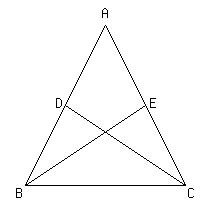

| 余白に記入 |
@2025 http://sugaku.club/
図形の性質と証明
定期試験対策テスト 5/14 ページ
7
次の問に答えなさい. [2K0-z1]
7
1点×4
次の図で,AB=BC=CAならば,∠A=∠B=∠Cであることを証明しなさい.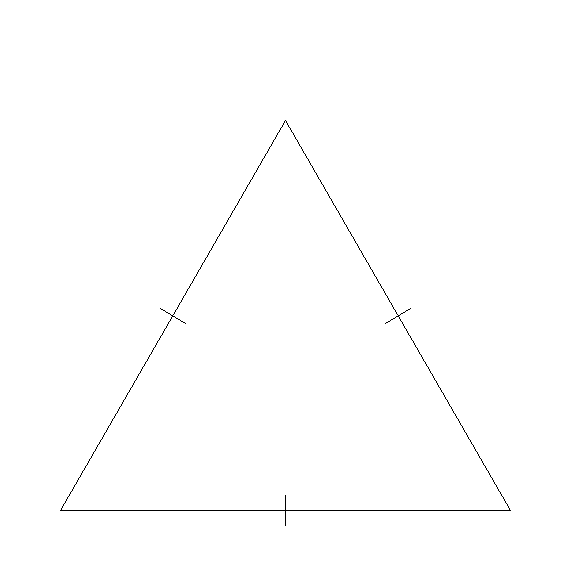
△ABCで,仮定より
AB=BC ---①
①から,△ABCはCAを底辺とする二等辺三角形なので
∠A= ---②
また,仮定より
AB=CA ---③
③から,△ABCはBCを底辺とする なので
∠B= ---④
② ④ から,
∠A=∠B=

A
B
C
△ABCで,仮定より
AB=BC ---①
①から,△ABCはCAを底辺とする二等辺三角形なので
∠A= ---②
また,仮定より
AB=CA ---③
③から,△ABCはBCを底辺とする なので
∠B= ---④
② ④ から,
∠A=∠B=
| 余白に記入 |
@2025 http://sugaku.club/
図形の性質と証明
定期試験対策テスト 6/14 ページ
8
次の問に答えなさい. [2K2-z0]
8
7点 部分点可
次の図で,△ABCは正三角形です.辺AB,BC,CA上に,AD=BE=CFとなるような点D,E,Fをとります.このとき,△DEFが正三角形になることを証明しなさい.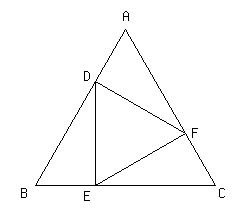

| 余白に記入 |
@2025 http://sugaku.club/
図形の性質と証明
定期試験対策テスト 7/14 ページ
9
次の問に答えなさい. [2L3-z1]
9
1点×5
次の図で,∠ADB=∠CDB,∠A=∠C=90°ならば,△ABD≡△CBDであることを証明しなさい.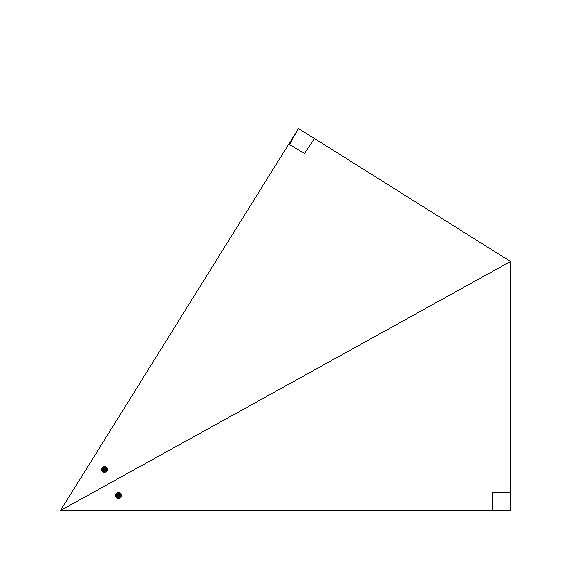
△ABDと△CBDで
仮定より,
∠ADB= ---①
∠A= ---②
また,BDは共通だから
BD= ---③
①②③ から, ので
△ABD≡

A
B
C
D
△ABDと△CBDで
仮定より,
∠ADB= ---①
∠A= ---②
また,BDは共通だから
BD= ---③
①②③ から, ので
△ABD≡
| 余白に記入 |
@2025 http://sugaku.club/
図形の性質と証明
定期試験対策テスト 8/14 ページ
10
次の問に答えなさい. [2L4-z0]
10
7点 部分点可
AB=ACの二等辺三角形ABCがあります.B,Cから,それぞれAC,ABに垂線BE,CDをひくとき,△DBC≡△ECBであることを証明しなさい.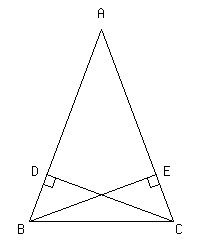

| 余白に記入 |
@2025 http://sugaku.club/
図形の性質と証明
定期試験対策テスト 9/14 ページ
11
次の問に答えなさい. [2M5-z0]
11
7点 部分点可
次の四角形ABCDで,BC//AD,BC=ADならば,四角形ABCDは平行四辺形であることを証明しなさい.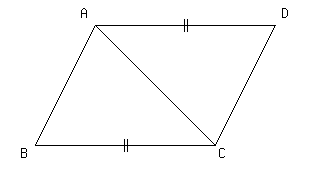

| 余白に記入 |
@2025 http://sugaku.club/
図形の性質と証明
定期試験対策テスト 10/14 ページ
12
次の問に答えなさい. [2M3-z0]
12
7点 部分点可
次の図で,△ABC≡△EDF,AC//EFならば,四角形BHDGは平行四辺形であることを証明しなさい.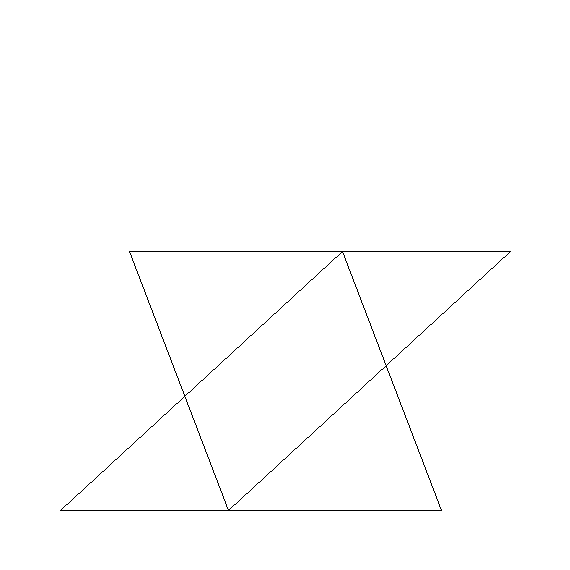

A
B
C
D
E
F
G
H
| 余白に記入 |
@2025 http://sugaku.club/
図形の性質と証明
定期試験対策テスト 11/14 ページ
13
次の問に答えなさい. [2N2-z0]
13
7点 部分点可
次の▱ABCDがAC⊥BDであるとき,▱ABCDはひし形となることを証明しなさい.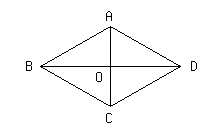

| 余白に記入 |
@2025 http://sugaku.club/
図形の性質と証明
定期試験対策テスト 12/14 ページ
14
次の問に答えなさい. [2P0-z1]
14
1点×4
次の図で,PQ//ABであるとき,△PAB=△QABとなることを証明しなさい.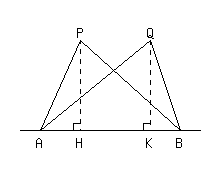
PQ//ABなので
PH=
△PABと で
底辺 は共通で,高さが等しいから は等しい.
よって
△PAB=△QAB

PQ//ABなので
PH=
△PABと で
底辺 は共通で,高さが等しいから は等しい.
よって
△PAB=△QAB
| 余白に記入 |
@2025 http://sugaku.club/
図形の性質と証明
定期試験対策テスト 13/14 ページ
15
次の問に答えなさい. [2P3-z0]
15
7点 部分点可
次の図で,DE//BCであるとき,△ABE=△ACDとなることを証明しなさい.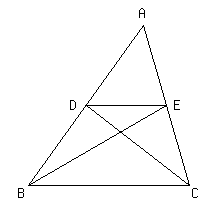

| 余白に記入 |
@2025 http://sugaku.club/
図形の性質と証明
定期試験対策テスト 14/14 ページ
16
次の問に答えなさい. [2P2-z0]
16
完答 6点
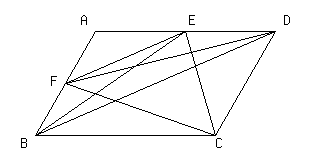 四角形ABCDは平行四辺形です.EF//BDのとき,△BCFと面積が等しい三角形をすべて見つけなさい.
四角形ABCDは平行四辺形です.EF//BDのとき,△BCFと面積が等しい三角形をすべて見つけなさい.
17
次の問に答えなさい. [2P1-z0]
17
6点
四角形ABCDで,辺ABをAの方向に延長した直線上に点Eをとり,△BCEの面積が,四角形ABCDの面積と等しくなるように,点Eの位置を求めて△BCEを三角定規を使って描きなさい.

A
B
C
D
| 図に記入 |
@2025 http://sugaku.club/
【解答例】
定期試験対策テスト 時間 60分 1/14 ページ
1
次の空欄に適する語を書きなさい.
1
1点×6
| 空欄に記入 |
2
下図の三角形の中から合同な三角形の組を選び,記号≡を使って表しなさい.また,合同条件を書きなさい. [2L5-00]
2
順不同 完答 2点×3
8cm A B 14cm C | 4cm 35° D E F | 7cm 60° G H I |
4cm 35° J K L | 7cm 60° M N O | 8cm P Q 14cm R |
| (1) | △DEF≡△JKL 1組の辺とその両端の角がそれぞれ等しい |
| (2) | △ABC≡△PQR 直角三角形の斜辺と他の1辺がそれぞれ等しい |
| (3) | △GHI≡△MNO 直角三角形の斜辺と1つの鋭角がそれぞれ等しい. |
@2025 http://sugaku.club/
【解答例】
定期試験対策テスト 2/14 ページ
3
次のことがらについて,逆を答えなさい.また,それが正しい場合には○,間違っている場合には×を( )に書きなさい.逆が間違っている場合に反例を書きなさい. [2J0-z3]
3
完答 1点×3
(1) 関数 y=3x−1 において x=1 ならば y=2 である.
(2) △ABCと△DEFについて AB=DE,BC=EF,AC=DF ならば △ABC≡△DEF である.
(3) △ABC≡△DEF ならば AB=DE である.
| (1) | 逆:関数 y=3x−1 において y=2 ならば x=1 である. (○) 反例: |
| (2) | 逆:△ABCと△DEFについて △ABC≡△DEF ならば AB=DE,BC=EF,AC=DF である. (○) 反例: |
| (3) | 逆:AB=DE ならば △ABC≡△DEF である. (×) 反例:BC≠EFの場合 |
4
次の空欄に適する語を書きなさい.
4
1点×4
| 空欄に記入 |
@2025 http://sugaku.club/
【解答例】
定期試験対策テスト 3/14 ページ
5
次の問に答えなさい. [2i0-z0]
5
7点 部分点可
次の図で,AB=CBならば,∠A=∠Cであることを証明しなさい.
ACの中点を点Dとおく
△ABDと△CBDで
点DはACの中点なので
AD=CD ---①
仮定より,
AB=CB ---②
また,BDは共通だから
BD=BD ---③
① ② ③ から, 3組の辺がそれぞれ等しい ので
△ABD≡△CBD
合同な図形では 対応する角の大きさは等しいので
∠A=∠C

A
B
C
D
ACの中点を点Dとおく
△ABDと△CBDで
点DはACの中点なので
AD=CD ---①
仮定より,
AB=CB ---②
また,BDは共通だから
BD=BD ---③
① ② ③ から, 3組の辺がそれぞれ等しい ので
△ABD≡△CBD
合同な図形では 対応する角の大きさは等しいので
∠A=∠C
| 空欄に記入 |
@2025 http://sugaku.club/
【解答例】
定期試験対策テスト 4/14 ページ
6
次の問に答えなさい. [2i2-z0]
6
7点 部分点可
△ABCの辺AB,AC上にそれぞれ点D,Eがあり,BD=CEとする.このとき,DC=EBならば,△ABCは二等辺三角形になることを証明しなさい.
△DBCと△ECBで
仮定より
BD=CE ---①
DC=EB ---②
BCは共通なので
BC=CB ---③
①②③より,3組の辺がそれぞれ等しいので
△DBC≡△ECB
合同な図形では,対応する角は等しいので
∠DBC=∠ECB
したがって,△ABCは二等辺三角形である.

△DBCと△ECBで
仮定より
BD=CE ---①
DC=EB ---②
BCは共通なので
BC=CB ---③
①②③より,3組の辺がそれぞれ等しいので
△DBC≡△ECB
合同な図形では,対応する角は等しいので
∠DBC=∠ECB
したがって,△ABCは二等辺三角形である.
| 余白に記入 |
@2025 http://sugaku.club/
【解答例】
定期試験対策テスト 5/14 ページ
7
次の問に答えなさい. [2K0-z1]
7
1点×4
次の図で,AB=BC=CAならば,∠A=∠B=∠Cであることを証明しなさい.
△ABCで,仮定より
AB=BC ---①
①から,△ABCはCAを底辺とする二等辺三角形なので
∠A= ∠C ---②
また,仮定より
AB=CA ---③
③から,△ABCはBCを底辺とする 二等辺三角形 なので
∠B= ∠C ---④
② ④ から,
∠A=∠B= ∠C

A
B
C
△ABCで,仮定より
AB=BC ---①
①から,△ABCはCAを底辺とする二等辺三角形なので
∠A= ∠C ---②
また,仮定より
AB=CA ---③
③から,△ABCはBCを底辺とする 二等辺三角形 なので
∠B= ∠C ---④
② ④ から,
∠A=∠B= ∠C
| 余白に記入 |
@2025 http://sugaku.club/
【解答例】
定期試験対策テスト 6/14 ページ
8
次の問に答えなさい. [2K2-z0]
8
7点 部分点可
次の図で,△ABCは正三角形です.辺AB,BC,CA上に,AD=BE=CFとなるような点D,E,Fをとります.このとき,△DEFが正三角形になることを証明しなさい.
△ADFと△BEDと△CFEで
仮定より
AB=BC=CA ---①
AD=BE=CF ---②
∠FAD=∠DBE=∠ECF=60° ---③
①②より
AF=BD=CE ---④
②③④より,2組の辺とその間の角がそれぞれ等しいので
△ADF≡△BED≡△CFE
したがって,
FD=DE=EF
3つの辺の長さが等しいので,△DEFは正三角形である.

△ADFと△BEDと△CFEで
仮定より
AB=BC=CA ---①
AD=BE=CF ---②
∠FAD=∠DBE=∠ECF=60° ---③
①②より
AF=BD=CE ---④
②③④より,2組の辺とその間の角がそれぞれ等しいので
△ADF≡△BED≡△CFE
したがって,
FD=DE=EF
3つの辺の長さが等しいので,△DEFは正三角形である.
| 余白に記入 |
@2025 http://sugaku.club/
【解答例】
定期試験対策テスト 7/14 ページ
9
次の問に答えなさい. [2L3-z1]
9
1点×5
次の図で,∠ADB=∠CDB,∠A=∠C=90°ならば,△ABD≡△CBDであることを証明しなさい.
△ABDと△CBDで
仮定より,
∠ADB= ∠CDB ---①
∠A= ∠C ---②
また,BDは共通だから
BD= BD ---③
①②③ から, 直角三角形の斜辺と1つの鋭角がそれぞれ等しい ので
△ABD≡ △CBD

A
B
C
D
△ABDと△CBDで
仮定より,
∠ADB= ∠CDB ---①
∠A= ∠C ---②
また,BDは共通だから
BD= BD ---③
①②③ から, 直角三角形の斜辺と1つの鋭角がそれぞれ等しい ので
△ABD≡ △CBD
| 余白に記入 |
@2025 http://sugaku.club/
【解答例】
定期試験対策テスト 8/14 ページ
10
次の問に答えなさい. [2L4-z0]
10
7点 部分点可
AB=ACの二等辺三角形ABCがあります.B,Cから,それぞれAC,ABに垂線BE,CDをひくとき,△DBC≡△ECBであることを証明しなさい.
△DBCと△ECBで
仮定より
∠BDC=∠CEB=90° ---①
△ABCは二等辺三角形なので
∠DBC=∠ECB ---②
BCは共通なので
BC=CB ---③
①②③より,直角三角形の斜辺と1つの鋭角がそれぞれ等しいので
△DBC≡△ECB

△DBCと△ECBで
仮定より
∠BDC=∠CEB=90° ---①
△ABCは二等辺三角形なので
∠DBC=∠ECB ---②
BCは共通なので
BC=CB ---③
①②③より,直角三角形の斜辺と1つの鋭角がそれぞれ等しいので
△DBC≡△ECB
| 余白に記入 |
@2025 http://sugaku.club/
【解答例】
定期試験対策テスト 9/14 ページ
11
次の問に答えなさい. [2M5-z0]
11
7点 部分点可
次の四角形ABCDで,BC//AD,BC=ADならば,四角形ABCDは平行四辺形であることを証明しなさい.
△ABCと△CDAで
仮定より
BC=AD ---①
BC//ADから平行線の錯角は等しいので
∠BCA=∠DAC ---②
また,ACは共通だから
AC=CA ---③
①②③ から,2組の辺とその間の角がそれぞれ等しいので
△ABC≡△CDA
合同な図形では 対応する辺は等しいので
AB=CD
四角形ABCDは,向かいあう辺が等しいので平行四辺形である

△ABCと△CDAで
仮定より
BC=AD ---①
BC//ADから平行線の錯角は等しいので
∠BCA=∠DAC ---②
また,ACは共通だから
AC=CA ---③
①②③ から,2組の辺とその間の角がそれぞれ等しいので
△ABC≡△CDA
合同な図形では 対応する辺は等しいので
AB=CD
四角形ABCDは,向かいあう辺が等しいので平行四辺形である
| 余白に記入 |
@2025 http://sugaku.club/
【解答例】
定期試験対策テスト 10/14 ページ
12
次の問に答えなさい. [2M3-z0]
12
7点 部分点可
次の図で,△ABC≡△EDF,AC//EFならば,四角形BHDGは平行四辺形であることを証明しなさい. AC//EFより,錯角は等しいので
AC//EFより,錯角は等しいので
∠A=∠FBG ---①
∠F=∠GDA ---②
△ABC≡△EDFより,合同な図形では 対応する角の大きさは等しいので
∠E=∠A ---③
∠F=∠C ---④
① ③ から,∠E=∠FBG ---⑤
② ④ から,∠C=∠GDA ---⑥
同位角の等しい2直線は 平行なので
⑤ から,DH//GB ---⑦
⑥ から,BH//GD ---⑧
⑦ ⑧ から,2組の向かい合う辺がそれぞれ平行なので,四角形BHDGは 平行四辺形である.

A
B
C
D
E
F
G
H
∠A=∠FBG ---①
∠F=∠GDA ---②
△ABC≡△EDFより,合同な図形では 対応する角の大きさは等しいので
∠E=∠A ---③
∠F=∠C ---④
① ③ から,∠E=∠FBG ---⑤
② ④ から,∠C=∠GDA ---⑥
同位角の等しい2直線は 平行なので
⑤ から,DH//GB ---⑦
⑥ から,BH//GD ---⑧
⑦ ⑧ から,2組の向かい合う辺がそれぞれ平行なので,四角形BHDGは 平行四辺形である.
| 余白に記入 |
@2025 http://sugaku.club/
【解答例】
定期試験対策テスト 11/14 ページ
13
次の問に答えなさい. [2N2-z0]
13
7点 部分点可
次の▱ABCDがAC⊥BDであるとき,▱ABCDはひし形となることを証明しなさい.
△ABOと△ADOで,仮定より
∠AOB=∠AOD=90° ---①
AOは共通だから
AO=AO ---②
平行四辺形の性質より
BO=DO ---③
① ② ③ から,2組の辺とその間の角がそれぞれ等しいので
△ABO≡△ADO
合同な図形では 対応する辺は等しいので
AB=AD ---④
平行四辺形の向かい合う辺は等しいから,④より,4つの辺はすべて等しくなる.したがって,四角形ABCDはひし形である.

△ABOと△ADOで,仮定より
∠AOB=∠AOD=90° ---①
AOは共通だから
AO=AO ---②
平行四辺形の性質より
BO=DO ---③
① ② ③ から,2組の辺とその間の角がそれぞれ等しいので
△ABO≡△ADO
合同な図形では 対応する辺は等しいので
AB=AD ---④
平行四辺形の向かい合う辺は等しいから,④より,4つの辺はすべて等しくなる.したがって,四角形ABCDはひし形である.
| 余白に記入 |
@2025 http://sugaku.club/
【解答例】
定期試験対策テスト 12/14 ページ
14
次の問に答えなさい. [2P0-z1]
14
1点×4
次の図で,PQ//ABであるとき,△PAB=△QABとなることを証明しなさい.
PQ//ABなので
PH= QK
△PABと △QAB で
底辺 AB は共通で,高さが等しいから 面積 は等しい.
よって
△PAB=△QAB

PQ//ABなので
PH= QK
△PABと △QAB で
底辺 AB は共通で,高さが等しいから 面積 は等しい.
よって
△PAB=△QAB
| 余白に記入 |
@2025 http://sugaku.club/
【解答例】
定期試験対策テスト 13/14 ページ
15
次の問に答えなさい. [2P3-z0]
15
7点 部分点可
次の図で,DE//BCであるとき,△ABE=△ACDとなることを証明しなさい.
△ABEは,△ADEと△DBEに分けられるので
△ABE=△ADE+△DBE ---①
△ADCは,△ADEと△DCEに分けられるので
△ADC=△ADE+△DCE ---②
DE//BCなので
△DEB=△DCE ---③
①②③より
△ABE=△ADC

△ABEは,△ADEと△DBEに分けられるので
△ABE=△ADE+△DBE ---①
△ADCは,△ADEと△DCEに分けられるので
△ADC=△ADE+△DCE ---②
DE//BCなので
△DEB=△DCE ---③
①②③より
△ABE=△ADC
| 余白に記入 |
@2025 http://sugaku.club/
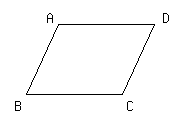 ▱ABCDについて,∠A=∠D,AB=BCのとき,この四角形は
▱ABCDについて,∠A=∠D,AB=BCのとき,この四角形は